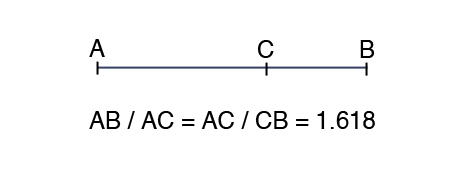I’ve started a series that I hope to continue and add to from time to time on the blog. It’s about this man George Packard, a retired schoolteacher, who lives in L.A. and who thinks and does many of the same things I do – except not exactly. Whaaaat??? Well, suffice it to say that George Packard provides me with a ticket to ride. Sort of a poetic license to play in traffic. And I must credit (or is it blame?) Eric Alagan and his fine Mechanic Leigh series for the idea of speaking my own thoughts in an approximate sort of way so as to create a character. In any case, poor Mr. Packard is occupied with much of the same nonsense as I, and I do feel sorry for him sometimes.
The George Packard Series
Chapter I
Mr. Packard, retired schoolteacher, was talking to himself again. Actually, he was reading out loud as he typed. He was transcribing onto his new Macintosh computer the text of some old math treatises he had saved.
“OK.” he announced, though no one was in the apartment, “Pi divided by two equals two divided by the square root of phi – to within a thousandth part. Hah!”
“Pi,” he read on, “can usefully be taken as four divided by the square root of phi.”
“I’ll definitely need to write that one out in symbols,” Packard said to himself.
So he did.
π/2 =2/√Ø
4/√Ø = π
But the equations that Packard, the retired schoolteacher, gazed at remained incomprehensible to him. It was because he could not picture the square root of a relationship. To visualize a squaring relationship was possible, a third dimension too was conceivable. But this inverse process, this taking of a square root, was harder to conceive. And how can a relationship have a root? What would it look like? For it seemed that unless he could visualize something, he could not understand it. This seemed to be his limitation in mathematics. The wall he always seemed to be hitting.
Packard lifted his heavy head from the equations he had Xeroxed a number of years earlier from John Anthony West’s book called Serpent in the Sky. These several tattered pages, which he had often times carried with him in his backpack or briefcase, and over which he had “wasted” many pleasant and enjoyable hours concerned the golden proportion phi. Phi, the golden proportion, was discussed and explanified in West’s book on Egyptology because phi was fundamental, according to the author, to understanding the architecture of ancient Egypt. In particular the design of the Great Pyramid.
Packard was perpetually fascinated by the Great Pyramid of Cheops. The pyramid’s base was, and still is, a nearly-perfect square whose perimeter is equal to the circumference of a circle whose radius is the pyramid’s height. Herodotus had recorded that relationship in his Histories. He had been informed of the Pyramid’s proportions by his 5th century B.C.E. tour guide. The golden proportion and its relation to the other great proportion, pi, was the key here to the Pyramid’s construction.
On the bottom of the page Packard puzzled over a footnote that stated that pi also equals phi squared times six fifths.
At then at the very bottom he read another footnote, which informed that four times the Great Pyramid’s base of 440 cubits equals 1760 cubits. The height of 280 cubits times 2 pi, or 22/7, equals 1760 square cubits.
Packard had been informally studying this jewel of mathematics for ten years. And now that he was retired, he had once again become immersed in thought and contemplation of this golden mean. Although he did not yet fully understand its more abstract operations (the square root of phi for instance), Packard still enjoyed contemplating its elegance: knowledge of phi had enabled the Egyptians of nearly five thousand years ago to build the Great Pyramid. This knowledge is everyone’s, he thought. Yet it seems to be no one’s. People forget so easily, or perhaps they simply don’t want to know. Civilizations rise and fall. Somewhere underneath the sands and smoldering wreckage of central Iraq, underneath some abandoned field, lie fragments of the Hanging Gardens of Babylon, thought Packard.
“And what are we to believe in today?” had asked some of his snottier little students on more than one occasion. It was a lament of today’s society. You heard it all the time. It was a widely-held complaint that there was nothing to believe in. People wanted so much to believe in something. It was a common sentiment. Often you would hear people say that it’s a good thing, nay a necessary thing, to believe in some God, some religion. His high school students would say things like: “Gee, Mr. Packard, how can the kids coming up today feel like they have a chance in their lives when there’s like nothing to believe in?” One time, Packard recalled with a chuckle, some kid, a tough, wise-ass from the back of the room retorted to one of the complainers: “Yeah? Well, why don’t you just open your eyes? Open your eyes. You see, man, I only believe in what I see. I don’t need to believe anything.”
OK, then. Packard, he himself, was free from believing. At age sixty-six, he had finally gotten past that barrier. But trying to understand things could also become a distraction. A final hurdle, or perhaps just another hurdle, for him to overcome on his long and winding spiritual quest. Packard hoped it would be a final barrier. He hoped he was getting close to a better understanding of the mathematics and geometry. Closer to enlightenment. And he hoped that one day soon he would finally be able to understand the golden proportion and the other great abstractions more fully. Whether he would obtain any benefit from understanding the world in this manner he did not know, but Packard was willing to find out. He was placing his bets on these mathematical epiphanies. It was such a pleasant path for him in any case. Let’s see….
If phi is the relationship between the larger to the smaller piece, the square root of phi would be …